Educational Codeforces Round 63

Posted on | | 阅读数 次
Words count in article: 2k | Reading time ≈ 10

F. Delivery Oligopoly

开启传送门

题目描述

The whole delivery market of Berland is controlled by two rival companies: BerEx and BerPS. They both provide fast and reliable delivery services across all the cities of Berland.

The map of Berland can be represented as an undirected graph. The cities are vertices and the roads are edges between them. Each pair of cities has no more than one road between them. Each road connects different cities.

BerEx and BerPS are so competitive that for each pair of cities $(v,u)$ they have set up their paths from $v$ to $u$ in such a way that these two paths don’t share a single road. It is guaranteed that it was possible.

Now Berland government decided to cut down the road maintenance cost by abandoning some roads. Obviously, they want to maintain as little roads as possible. However, they don’t want to break the entire delivery system. So BerEx and BerPS should still be able to have their paths between every pair of cities non-intersecting.

What is the minimal number of roads Berland government can maintain?

More formally, given a 2-edge connected undirected graph, what is the minimum number of edges that can be left in it so that the resulting graph is also 2-edge connected?

Input

The first line contains two integers $n$ and $m$ ($3\leq n\leq14$, $n\leq m\leq \frac{n(n-1)}{2}$) — the number of cities and the number of roads between them.

Each of the next 𝑚 lines contains two integers $v$ and $u$ ($1\leq v,u\leq n,v\neq u$) — the cities connected by the next road.

It is guaranteed that each pair of cities has no more than one road between them. It is guaranteed that each pair of cities have at least two paths between them that don’t share a single road.

Output

The first line should contain a single integer $k$ — the minimum number of roads Berland government can maintain so that BerEx and BerPS are still able to have their paths between every pair of cities non-intersecting.

The next $k$ lines should contain the list of roads which are being maintained. Each line of form “$v\ u$”, where $v$ and $u$ are cities connected by the next road.

If there are multiple lists of minimum size, print any of them. The order of roads in the list doesn’t matter.

Examples

input1

3 3
1 2
2 3
3 1

output1

3
1 3
3 2
1 2

input2

4 5
1 2
1 4
2 3
4 3
1 3

output2

4
1 4
4 3
3 2
1 2

input3

6 10
1 2
2 3
3 1
3 4
4 5
5 6
4 6
2 5
1 6
3 5

output3

6
1 6
6 5
5 4
4 3
3 2
1 2

Note

Here are graphs from the examples, red edges are the maintained ones.

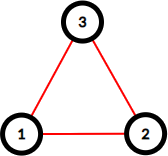
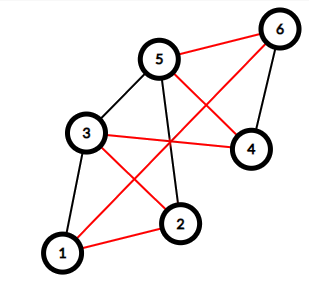
cf_1155_f_1.png

cf_1155_f_1.png

cf_1155_f_1.png

题意

给你一个不超过14个节点的无向图，让你找到满足一下条件的一个子图：

  • 包含所有点
  • 包含尽可能少的边
  • 子图中任意两个点存在两条完全不交的路径

让你输出一个任意符合题意的子图。

分析

当时没做出来，看题解才做出来的。建议先看原题解。如下：

Let’s use dynamic programming to solve this problem. We will start with a single biconnected component consisting of vertex $0$, and connect other vertices to it. So, the state of our dynamic programming will be a $mask$ of vertices that are in the same biconnected component with $0$.

How can we extend a biconnected component in such a way that some other vertices are added into it, but it is still biconnected? We will add a path (possibly cyclic) that starts in some vertex $x$ belonging to the $mask$, goes through some vertices not belonging to the $mask$, and ends in some vertex $y$ belonging to the $mask$ (possibly $x=y$). If for every triple ($x,y,addmask$) we precalculate some path that starts in $x$, goes through vertices from $addmask$ and ends in $y$ (and $addmask$ does not contain neither $x$ nor $y$), then we can solve the problem in $O(3^nn^2)$: there will be $2^n$ states, for every state we will iterate on two vertices $x$ and $y$ belonging to the $mask$, and the number of possible pairs of non-intersecting masks $mask$ and $addmask$ is $O(3^n)$.

The only thing that’s left is precalculating the paths for triples ($x,y,addmask$). That can be done with auxiliary dynamic programming $dp2[x][y][addmask]$ which will denote whether such a path exists. For every edge ($u,v$) of the original graph, $dp2[u][v][0]$ is true, and we can go from $dp2[x][y][addmask]$ to some state $dp2[x][z][addmask^{‘}]$, where $addmask^{‘}$ will contain all vertices from $addmask$ and vertex $y$ (and we should ensure that there is an edge ($y,z$) in the graph and the $addmask$ didn’t contain vertex $y$ earlier). We should also somehow be able to restore the paths from this dp, and we also should be careful not to choose the same edge twice (for example, if we start a path by edge ($x,y$), we should not use the same edge to return to $x$) — both these things can be done, for example, by storing next-to-last vertex in the path.

我基本是看完题解才有想法的，和题解写的一模一样，（其实不一样，我写的比标程丑）。

大体思路还是很清晰的。

首先，我们可以很轻松的发现，答案一定是很多环交在了一起构成了答案对应的子图，然后对于任何一个存在很多环相交的图来说，我们可以拆成一个环和很多很多边构成的，如下图：

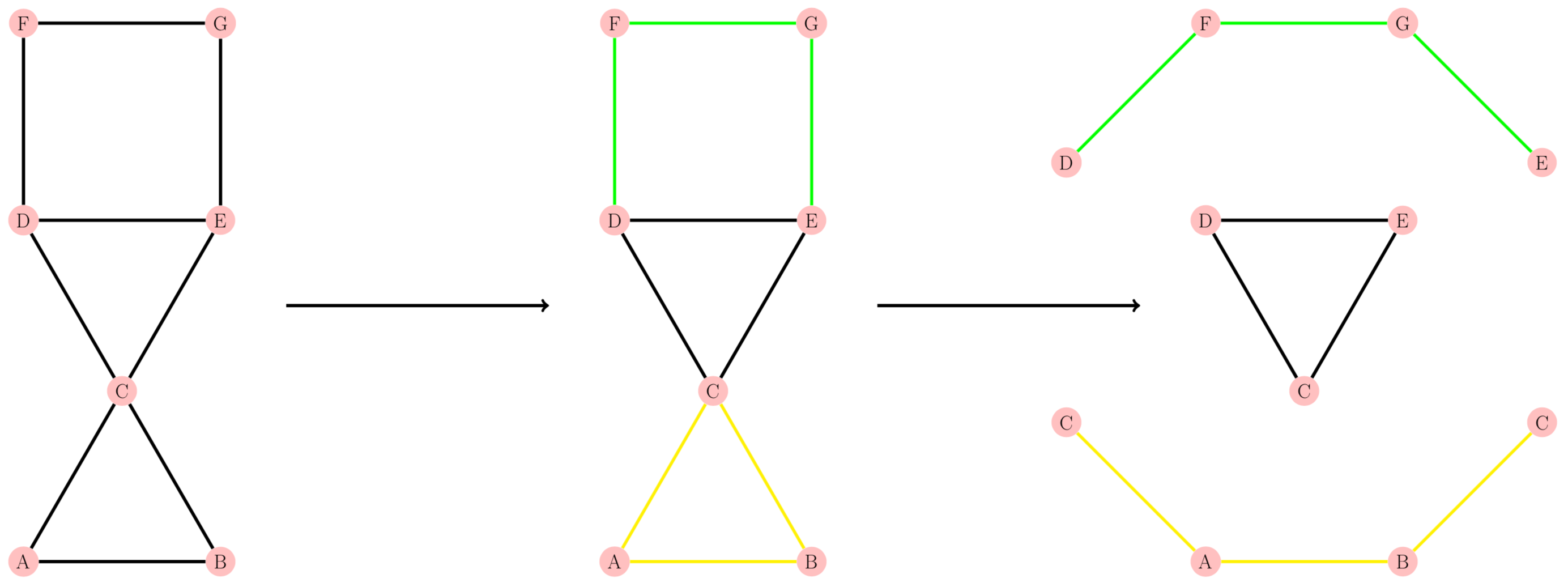
edu_cf_63_f_1.png

同样的我们可以很轻松的得到，任何一个环都可以作为拆分后唯一的环。剩下的问题就是我们怎么找到所有的边了。也即怎么找到我们需要的所有路径。我们做以下定义。

我们找到一条从$a$到$b$的路径，并且其中包括$mask$对应的其他点，我们假设$dp2[a][b][mask]$表示是否存在一条从$a$到$b$的路径，并且还包含了$mask$点，例如：

$dp2[1][3][1] = 1$表示存在一条$1-0-3$的路径

$dp2[3][5][3] = 1$表示存在一条从$3$到$5$的路径，其中包含$0$号点和$1$号点，路径可能是$3-0-1-5$，也可能是$3-1-0-5$。

对于他的转移显然比较好想，直接枚举下一个点是谁就行了。

然后我们取出任意一个节点表示当前符合答案的子图的子图。因为一个点的时候显然符合答案（因为一对都没有）。然后我们在这个子图的子图中不断的添加边构成环，最后判断得到的全图是否满足答案就行了。。。。

代码

给大佬递上我奇丑无比的代码　(/ω＼)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include<bits/stdc++.h>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 14;
const int maxm = 1<<maxn;
int n,m,upper;
int dp[maxm|10];//记录答案是否存在，也即当前子图是否满足条件（子图中任意两个点存在两条完全不交的路径）
bool dp2[maxn][maxn][maxm];//表示是否存在一条从i到j，包含mask对应点的路径
int last[maxn][maxn][maxm];//用来记录i到j中上一个点是谁，用来输出路径
vector<int> bit[maxm|10];//表示mask中对应的点的编号
vector<int> mat[maxm|10];//存输入的图
pair<int,int> con[maxm|10];//表示mask对应的两个外部点，也就是路径的起点终点
int addmask[maxm|10];//mask对应的外部边对应的mask
void show_bit(int a){
	if(a) show_bit(a>>1);
	else return ;
	if(a&1) cout<<1;
	else cout<<0;
}
int main(){
	cin>>n>>m;
	upper = 1<<n;
	for(int i = 0,a,b;i<m;i++){
		cin>>a>>b;
		a--,b--;
		mat[a].push_back(b);
		mat[b].push_back(a);
	}
	memset(dp,0x3f,sizeof dp);
	memset(dp2,false,sizeof dp2);
	for(int i = 0;i<n;i++)
		for(auto j: mat[i]){
			dp2[i][j][0] = 1;
			last[i][j][0] = i;
		}
	for(int mask = 0;mask<upper;mask++) for(int j = 0;j<n;j++) if(mask&(1<<j)) bit[mask].push_back(j);
	for(int mask = 0;mask<upper;mask++){
		for(int i = 0;i<n;i++){
			if(mask&(1<<i)) continue;
			for(int j = 0;j<n;j++){
				if(mask&(1<<j)) continue;
				if(i==j||dp2[i][j][mask]==false) continue;
				for(auto z:mat[j]){
					if(mask&(1<<z)) continue;
					if(z==last[i][j][mask]) continue;
					if(dp2[i][z][mask|(1<<j)]==false){
						last[i][z][mask|(1<<j)] = j;
						dp2[i][z][mask|(1<<j)] = true;
					}
				}
			}
		}
	}
	dp[1] = 0;
	for(int mask = 0;mask < upper;mask++) {
		for(int add = mask;add;add = (add-1)&mask){
			int pre = add^mask;
			int cnt = __builtin_popcount(add)+1;
			if(dp[pre]+cnt>=dp[mask]) continue;
			bool flag = false;
			for(auto x:bit[pre]){
				for(auto y: bit[pre]){
					if(dp2[x][y][add]){
						dp[mask] = dp[pre]+cnt;
						con[mask] = make_pair(x,y);
						addmask[mask] = add;
					}
				}
			}
		}
	}
	if(dp[(1<<n)-1]==inf) cout<<-1<<endl;
	else {
		cout<<dp[(1<<n)-1]<<endl;
		int cur = (1<<n) - 1;
		while(cur!=1){
			int add = addmask[cur];
			int x = con[cur].first;
			int y = con[cur].second;
			cur^=add;
			while(add){
				int ny = last[x][y][add];
				cout<<y+1<<' '<<ny+1<<endl;
				y = ny;
				add^=(1<<ny);
			}
			cout<<x+1<<' '<<y+1<<endl;
		}
	}
	return 0;
}